
ยินดีต้อนรับ เข้าสู่ระบบ เว็บแทงหวยออนไลน์ที่นิยมอันดับ 1ของเมืองไทย
แทงหวยออนไลน์ กับ 999LUCKY เว็บแทงหวยออนไลน์ ที่ครองใจคนทั้งประเทศ บริการแทงหวยออนไลน์ทุกชนิดครวนจรหวยที่เว็บนี้เว็บเดียว รองรับการเล่นทุกรูปแบบมีระบบฝาก-ถอนเงิน อัตโนมัติทันสมัยรวดเร็วทันใจสะดวกสบายที่สุด
999Lucky เราเปิดให้บริการมายาวนานมากกว่า10ปี จึงเป็นที่ยอมรับขอคอหวยเป็นอย่างมาก เราจะยำพนักงานเรื่องการดูแลให้บริการลูกค้าต้องมาก่อนเป็นหลักดูแลด้วยจริงใจใสใจทุกการเคลื่อนไหว ไม่ว่าจะชาติไหนเพราะท่านคือหนึ่งในครอบครัวเรา
ฝาก-ถอนง่ายไม่ต้องรอพนักงานยืนยันมีระบบอัพเดทเว็บไซต์ที่ทันสมัยรวดเร็วที่สุดอีกด้วย เชื่อถือได้ มั่นคง จ่ายจริง ไม่โกง โปร่งใส ปลอดภัยแน่นอน เรามีทีมงานมืออาชีพมากประสบการณ์ทางด้านหวยออนไลน์ทุกตัว
และถ้าท่านยังไม่เข้าใจ หรือสงสัยอะไร สามารถแจ้งติดต่อเรา ได้ในทันทีและยังอัพเดทตรางวัล ผลหวยต่างๆได้อย่างแม่นยำและรวดเร็วสุดๆอีกด้วย ตรวจหวยย้อนหลัง ได้ทุกตัวที่หน้าเว็บไซต์หลักของเราได้เลย
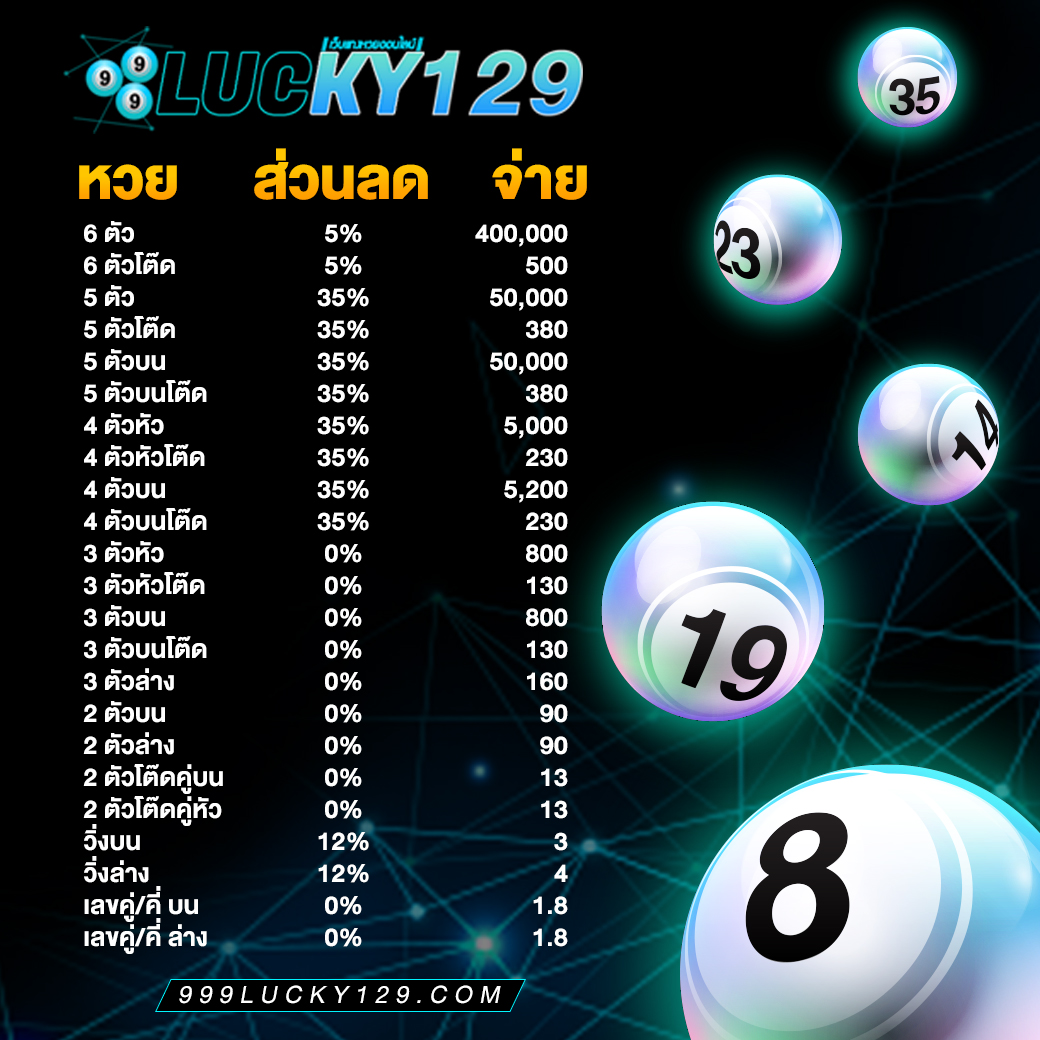
ระบบทำงานของ 999Lucky ดียังไง
- ระบบฝาก-ถอนเงินอัตโนมัติทันสมัยรวดเร็วทันใจ
- ระบบรองรับแทงหวยออนไลน์อย่างเต็มรูปแบบ
- ระบบรักษาความปลอดภัยสูงกว่าเว็บหวยอื่นๆ
- ระบบสำรองข้อมูลลูกค้าทุกท่าน แบบ Ail Time ไม่ต้องกังวนเรื่องเครดิตจะหาย
- ระบบ Cloud server เต็มรูปแบบ
- ระบบ ติดต่อเรา ได้ตลอด 24 ช.ม
หายห่วงเรื่องโดนแฮกเรื่องข้อมูลและบัญชีลูกค้าทุกท่านปลอดภัยแน่นอน เรามีทีมงานโปรแกรมเมอร์มืออาชีพมากประสบการณ์คอยดูแลและให้คำปรึกษาปัญหาต่างๆ ไม่ว่าจะเกิดปัญหาอะไรขึ้นเราสามารถแก้ไขปัญหาไม่เกิน 5นาที สบายใจได้ท่านจะได้เงินครบทุกบาท เราการันตีเลย ในกรณีเว็บไซต์มีปัญหาทางเรารับผิดชอบทั้งหมดเอง เชื่อมั่นได้กับ 999Lucky
เว็บแทงหวยออนไลน์ กับ 999Lucky มีบริการครบทุกหวยที่เว็บนี้เท่านั้น
- หวยรัฐบาลไทย
- หวยฮานอย
- หวยมาเลย์
- หวยจับยี่กี
- หวยใต้ดิน
- หวยลาว
- หวยเวียดนาม
- หวยหุ้นไทย
- หวยหุ้นต่างประเทศ
- หวยหุ้นดาวโจนส์
- หวยลัคกี้เฮง(หวยน้องใหม่)
บริการประทับใจ ดูแลใส่ใจเหมือนครอบครัว 999LUCKY เราเท่านั้น
โปรโมชั่น ติดต่อเรา สมัครสมาชิก
โบนัสและสิทธิพิเศษ กับ AFF แนะนำเพื่อนมาร่วกิจกรรมรับโบนัส 5%
ครบวนจรหวยออนไลน์ 999LUCKY เว็บแทงหวยที่ดีที่สุด ชื่อนี้เท่านั้น
